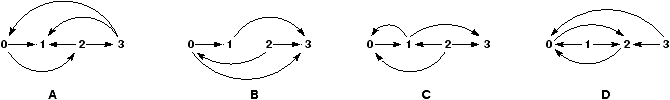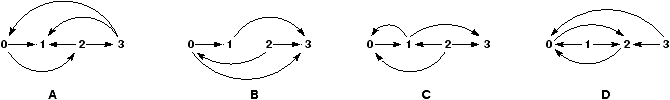TD 8 : Introduction aux graphes

EXERCICE 1

Soit G = (S,A) un graphe orienté et p un sommet de G. On dit que p est un puits si, pour tout sommet u différent de p, (u,p) Î A et (p,u) Ï A. Par exemple, parmi les quatre graphes suivants, A possède un puits (le sommet 1), B possède un puits (le sommet 3) mais C et D n'admettent pas de puits :

· Démontrez que si le graphe G admet un puits, alors il est unique.

· Ecrivez une méthode qui, étant donné deux tableaux de et ds, mets à jour ces tableaux tel que l'on ait de[u] = d_e(u) et ds[u] = d_s(u) pour tout u sommet du graphe, où d_e(u) (resp. d_s(u)) est le degré entrant (resp. le degré sortant) de u.

· Déduisez de ce qui précède un algorithme qui retourne le puits d'un graphe orienté s'il existe.

EXERCICE 2

On s'intéresse aux composantes connexes d'un graphe non orienté.

· Donnez un algorithme qui détermine le nombre de composantes connexes d'un graphe non orienté, et qui attribue à chaque sommet du graphe sa composante connexe, par exemple en retournant un tableau cc tel que cc[u] = k indique que le sommet u est dans la composante connexe k.

EXERCICE 3

On veut déterminer si un graphe orienté est acyclique, c'est à dire s'il ne contient aucun cycle.

· Etant donné un graphe orienté, écrivez un algorithme qui décide si le graphe est acyclique ou non.

· Même question que précédemment quand le graphe est non orienté.

EXERCICE 4

On considère les graphes suivants :

· Pour chacun de ces graphes, effectuez tous les parcours en profondeur possibles et dessinez pour chacun le graphe de liaison correspondant en donnant le type de tout ses arcs.

EXERCICE 5

On considère un graphe orienté G. Dans le parcours en profondeur générique, on ne discerne pas les arcs croisés des arcs couvrants.

· En utilisant un attribut supplémentaire, modifiez le parcours en profondeur générique afin qu'il affiche le type exact de chaque arc du parcours.

EXERCICE 6

Un graphe non orienté G = (S,A) est biparti s'il existe deux sous-ensembles S₁ et S₂ vérifiant S₁ ¹ Ø,

S₂ ¹ Ø, S₁ ÈS₂ = S et S₁ ÇS₂ = Ø tels que " u,v Î S, (u,v) Î A ÜÞ u Î S₁ et v Î S₂, ou u Î S₂ et v Î S₁

· Dessinez un graphe biparti.

· Donnez un algorithme qui décide si un graphe non orienté est biparti ou non.

EXERCICE 7

Soit G = (S,A) un graphe orienté. Un sommet u de S est une racine de G si pour tout sommet v différent de u il existe un chemin allant de u à v.

· Donnez un algorithme qui détermine si un graphe orienté possède au moins une racine, et si oui retourne une de ces racines.

EXERCICE 8

Soit G = (S,A) un graphe. On appelle base de G tout sous-ensemble B de S ayant les deux propriétés suivantes :

pour tout sommet u de S, il existe un sommet v de B tel qu'il existe un chemin (éventuellement de longueur 0) allant de v à u
B est minimal en taille, ce qui veut dire que tout sous-ensemble B' de S ayant la propriété précédente est tel que Card(B') ³ Card(B) (où Card(A) est le cardinal de l'ensemble A)

Par exemple, l'ensemble de sommet {0,2} est l'unique base du graphe G₅ de l'exercice 4 et les ensembles de sommet {0,5}, {2,5} et {4,5} sont les trois bases du graphe G₄ de l'exercice 4.

· Quel est le nombre minimum et maximum de base que peut admettre un graphe orienté d'ordre n et pour quel(s) graphe(s) ces valeurs sont-elles atteintes ?

· Soit G = (S,A) un graphe orienté. Démontrez les trois propriétés suivantes :

si le degré entrant d'un sommet u de S est nul, alors pour toute base B de G, u Î B
si le degré entrant d'un sommet u de S n'est pas nul et si u n'est pas dans un cycle, alors pour toute base B de G, u Ï B
Soit B une base de G et v un élément de B. Si un sommet u de S - B est tel que u et v sont dans le même cycle, alors B' = ( B - {v} ) È {u} est une base de G

Supposons maintenant qu'on effectue un parcours en profondeur d'un graphe G = (S,A), et que, durant ce parcours, on calcule pour tout sommet u de S la valeur f[u] qui est la date de fin de traitement de u. Soit w le sommet de S tel que f[w] est maximum.

· Démontrez qu'il existe une base B de G telle que w Î B

· Déduisez de la question précédente un algorithme qui, étant donné un graphe G = (S,A), trouve une base de G en effectuant deux parcours en profondeur.

EXERCICE 9

On considère les graphes de l'exercice 4.

· Pour chacun de ces graphes, effectuez plusieurs parcours en largeur en choisissant plusieurs sources différentes et calculez pour chacun d(s,u), la distance de plus court chemin en nombre d'arêtes entre la source s et tous les sommets u du graphe.

EXERCICE 10

Soit G = (S,A) un graphe non orienté qui est un arbre. On définit le diamètre d de G par d(G) = max{d(u,v) | u,v Î S} où d est la distance de plus court chemin en nombre d'arêtes. Autrement dit, le diamètre de G est la plus grande de toutes des distances de plus courts chemins en nombre d'arêtes dans G.

· Donnez un algorithme qui calcule le diamètre de G.

EXERCICE 11

On s'intéresse à un nouvel algorithme pour tester si un graphe non orienté est biparti (voir exercice 6)

· Donnez un algorithme basé sur le parcours en largeur qui décide si un graphe non orienté est biparti ou non.

EXERCICE 12

Soit G = (S,A) un graphe non orienté connexe. Un sommet u de S est un point d'articulation si, lorsqu'on supprime u (et les arêtes incidentes à u) dans G, le graphe résultant n'est plus connexe. Plus précisément, un sommet u de S est un point d'articulation si et seulement si u possède au moins deux sommets adjacents x et y tels que l'unique chemin reliant x et y dans G est celui qui passe par u.

Soit G = (S,A) un graphe non orienté connexe, et p un parcours en profondeur de G. On dit qu'un sommet u de S remonte strictement dans G_p (le graphe de liaison) si et seulement s'il existe une arête retour dans G_p partant de u ou d'un de ses descendants, et arrivant à un ancêtre propre de p[u]. Remarquez que ni la racine de G_p ni aucun de ses fils ne remontent strictement.

· Prouvez que le sommet r racine de G_p est un point d'articulation si et seulement si r possède au moins deux fils dans G_p.

· Prouvez qu'un sommet u différent de la racine de G_p est un point d'articulation si et seulement si u possède au moins un fils dans G_p qui ne remonte pas strictement.

Pour tout sommet u de S, on considère les attributs p[u] et d[u] du parcours p qui sont respectivement le père de u et la date de découverte de u dans G_p. On considère, pour tout sommet u de S, l'ensemble D(u) égal à l'ensemble contenant u lui-même, tous ses descendants dans G_p et tous les sommets extrémités d'une arête retour de G_p ayant pour origine u ou un de ses descendants dans G_p. On définit le nouvel attribut m[u] de p pour tout sommet u de S par m[u] = min{ d[v] | v Î D(u) }.

· Pour tout sommet u de S, prouvez que : u remonte strictement dans G_p ÜÞ m[u]<d[p[u]].

· Ecrivez la classe Articulation et la méthode afficher qui affiche sur le flux de sortie tous les points d'articulation de G.

EXERCICE 13

Dans la suite, on entend par graphe un graphe orienté. Un graphe G = (S,A) est dit semi-connexe si, pour toutes les couples de sommets u et v de S, il existe un chemin allant de u à v ou de v à u (le ou est non exclusif).

· Démontrez les propriétés suivantes :

un graphe acyclique G est semi-connexe ÜÞ il existe un chemin élémentaire dans G constitué de tous les sommets de G
un graphe G est semi-connexe ÜÞ le graphe réduit de G est semi-connexe
un graphe G est semi-connexe ÜÞ le graphe transposé G^t est semi-connexe

· Déduisez des questions précédentes un algorithme qui teste si un graphe quelconque est semi-connexe.

EXERCICE 14

Soit G = (S,A) un graphe non orienté valué et non (nécessairement) connexe. Une forêt couvrante de poids minimum de G (FCM dans la suite) est un graphe non orienté acyclique F = (S,A') tel que A' est l'union des ensembles d'arêtes des arbres couvrants de poids minimum des composantes connexes de G. On s'intéresse à la construction d'une telle forêt.

· Les algorithmes de Prim et de Kruskal donnent-ils une FCM si on les applique tels quels à un graphe non orienté valué non connexe ? Dans la négative, quelles sont les modifications à apporter à ces algorithmes pour qu'ils fabriquent une FCM ?

· Ecrivez les algorithmes de Prim et de Kruskal ainsi modifiés.

EXERCICE 15

Soit G = (S,A) un graphe non orienté connexe valué. On s'intéresse à l'unicité d'un arbre couvrant de poids minimum (ACM dans la suite) de G.

· Montrez par l'absurde, et en utilisant les propriétés des ACM, que si les poids des arêtes de G sont tous distincts, alors il n'existe qu'un seul ACM de G.

· Déduisez de la démonstration précédente une condition nécessaire pour qu'il existe plus d'un ACM pour un graphe donné, et montrez sur un exemple que cette condition n'est pas suffisante.

EXERCICE 16

Soit G = (S,A) un graphe non orienté connexe et valué, et soit T un ACM de G. On cherche un algorithme efficace pour mettre à jour T après l'ajout d'une nouvelle arête à G.

· Etant donné un arbre valué T = (S,A'), un sommet d (comme départ) et un sommet a (comme arrivée) de S, écrivez une méthode qui cherche et retourne l'arête de poids maximum parmi les toutes arêtes constituant le chemin (unique) de d à a dans T.

· En vous inspirant de l'exercice précédent et en utilisant la méthode de la question précédente, écrivez une méthode qui, étant donné G = (S,A) un graphe non orienté connexe et valué, T = (S,A') un ACM de G et (u,v) Ï A, met à jour T pour qu'il soit un ACM de G = (S,AÈ{(u,v)})

EXERCICE 17

Soit G = (S,A) un graphe non orienté connexe et valué ne possédant aucun pont, et soit T un ACM de G. On cherche un algorithme efficace pour mettre à jour T après la suppression d'une arête à G.

· Etant donné T = (S',A') un sous-graphe de G qui est un arbre, écrivez une méthode qui retourne l'arête de poids minimum parmi toutes les arêtes qui traverse S'.

· En utilisant les propriétés des ACM et à l'aide de la méthode précédente, écrivez une méthode qui, étant donné G = (S,A) un graphe non orienté connexe et valué, T = (S,A') un ACM de G et (u,v) Î A, met à jour T pour qu'il soit un ACM de G = (S,A-{(u,v)})

· Que peut-il se passer si le graphe G possède un ou plusieurs ponts ? En quoi consiste alors la mise à jour de T ?

EXERCICE 18

Un lotissement en construction peut être modelisé par un graphe non orienté connexe valué. Les sommets du graphe représentent les maisons du lotissement et les arêtes des conduits par lesquels on peut faire passer des câbles électriques, la valuation d'une arête étant simplement la longueur du conduit. On cherche à relier toutes les maisons au réseau électrique en minimisant la longueur totale des câbles. On dispose d'un certain nombre de sources électriques qui arrivent directement à certaines maisons. 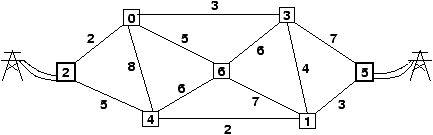Par exemple, dans le graphe suivant :

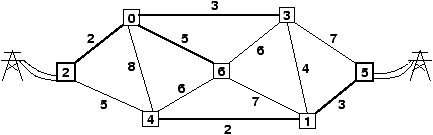
les maisons 2 et 5 sont directement reliées au réseau électrique. Chaque maison doit être reliée au réseau électrique une et une seule fois. Ce problème est très proche du problème de la recherche d'un arbre couvrant de poids minimum. La connection à moindre coût de l'ensemble des maisons du graphe précédent au réseau électrique est assurée en choisissant les arêtes en gras suivantes :

On remarque que l'ensemble des arêtes choisies (la solution) ne forme pas un arbre couvrant de poids minimum (ACM dans la suite) mais une forêt couvrante de poids minimum avec sources (FCM dans la suite). On remarque enfin que la FCM solution est obtenue en retirant l'arête (1,3) à l'unique ACM du graphe.

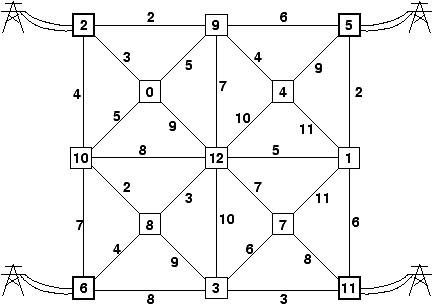
· En adaptant un algorithme étudié en cours, concevez un nouvel algorithme qui calcule une FCM d'un graphe non orienté connexe valué avec sources, et testez-le sur le graphe suivant dont les sources sont les sommets 2, 5, 6 et 11 :

· Ecrivez la classe FCMAvecSources qui exporte la méthode publique fcm, méthode qui calcule une FCM pour un graphe non orienté connexe valué avec sources.

This document was translated from L^AT_EX by H^EV^EA.