Mathématiques Discrètes
2005-2006

Mini Projet Mathématiques Discrètes
ESSI 1
Courbes récursives
Vous devez rendre ce projet au plus tard le Vendredi 10 Décembre 2004 à 18h. Au delà le répertoire de rendu est fermé. Rien ne vous interdit de rendre avant.
Les noms des fichiers qui vous sont donnés ici doivent être impérativement respectés.
Le protocole de rendu de projet sera le protocole standard pour tous les mini projets de l'année.
Le forum Projets ESSI1 est là pour que vous y posiez vos questions concernant ce projet. Aucune réponse ne sera faite à des questions posées par mail, afin que tous les étudiants bénéficient des mêmes renseignements.
Vous devez travailler en binome : votre binome doit être dans le même groupe de TD que vous. Si le groupe de TD comporte un nombre impair d'étudiants, il doit y avoir au choix un monome ou un trinome. Les binomes doivent être différents de ceux des mini projets précédents.
La liste des binômes par groupe de TD devra nous etre envoyé par mail, au plus tard le 24 Novembre (merci aux délégués de centraliser l'information)
Remarque : Vous serez noté sur vos réponses aux questions posées, et non sur d'éventuels enjolivements.
Le but de ce projet est d'étudier et de dessiner certaines courbes récursives. Ces familles sont définies par
- une courbe initiale T 1
- une règle de transformation qui permet de définit T k+1 en fonction de T k
I- Première famille C k :
Courbe initiale : C 1: Un segment défini par les coordonnées de ses deux extrémités.
Règle de transformation : On obtient C k+1à partir de C k en remplaçant chaque segment s de C k par les deux autres cotés du triangle rectangle isocèle dont s est la base, et en conservant toujours la même orientation..
Voici C 1,C2, C 3 et C 4
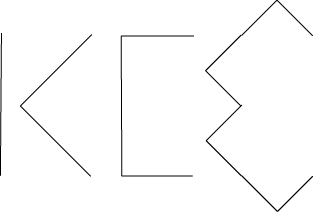
- Etablir et résoudre une relation de récurrence permettant de déterminer la longueur d'une telle courbe (la longueur étant la somme des longueurs des segments de droites qui constituent le dessin), en fonction de longueur du segment initial et de k.
- Ecrire une méthode récursive pour dessiner C k.. Pour cela, créer une classe CkSol qui étend la classe (abstraite)Ck (fichier Ck.java), en implémentant la méthode drawCk. Vous ne devez en aucun cas modifier la classe Ck. Un fichier TestCk.java vous est donné pour tester votre implémentation. Pour dessiner, vous allez utiliser uniquement la méthode Graphics.drawLine( int x1, int y1, int x2, int y2), qui trace un segment de droite entre les deux points de coordonnées (x1,y1) et (x2,y2). Rappelons que le point (0,0) est celui qui est en haut et à gauche, et non pas en bas à gauche comme on en a l'habitude en mathématiques. Voici par exemple, comment dessiner un rectangle .
- Déterminer la complexité de votre méthode drawCk. Pour vos calcul de complexité, vous supposerez que la méthode drawLine est exécutée en temps constant.
A RENDRE |
|
II- Deuxième famille H k
Courbe initiale :
Partager un carré en 4 "petits" carrés "égaux" ; numéroter chacun de ces carrés de sorte que deux carrés successifs se touchent par un côté, en commençant par le carré en bas à gauche, et terminant par le carré en bas à droite. H 1est la courbe obtenue en joignant les centres de ces carrés dans l'ordre 1,2,3,4
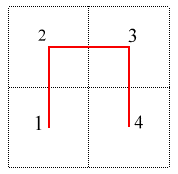
Pour obtenir H 2 , partager chacun de ces petits carrés en 4 "micro-carrés" "égaux", plus petits ; et numéroter chacun de ces micro-carrés de sorte que deux de ces micro-carrés successifs se touchent par un côté, en commençant par le micro-carré en bas à gauche, et terminant par le micro-carré en bas à droite, le premier micro-carré d'un petit carré devant avoir un côté en commun avec le dernier micro-carré du petit carré précédent et le dernier micro-carré devant toucher par un coté le petit carré suivant.
En reliant les centres des microcarrés dans l'ordre de leur numérotation, on obtient H 2
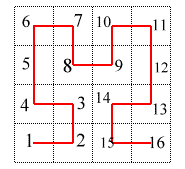
On construit de même H 3 et H 4
. 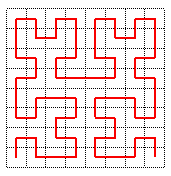

A l'étape n , on obtient donc une suite de 4 n carrés Cn,0,Cn,1,...Cn,4n-1, de côté 1/2n, deux carrés successifs se touchant par un côté, recouvrant successivement les carrés Cn-1,0,Cn-1,1,...Cn-1,4n-1-1, .
H nest la courbe obtnue en reliant les centres successifs des carrés

Le labyrinthe Ln est la réunion des côtés des carrés Cn,0,Cn,1,...Cn,4n-1, excepté les côtés joignant deux carrés consécutifs (et les deux entrées) :


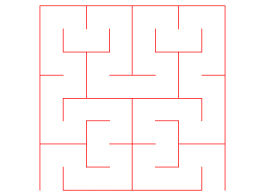
- Poser et résoudre l'équation de récurrence qui permet de calculer la longueur de H k, en fonction de la longueur de H1. La longueur d'une courbe étant la somme des longueurs des segments qui la compose.
- Ecrire une méthode récursive pour dessiner H k..
- Déterminer la complexité de votre méthode de dessin.
- Ecrire une méthode récursive pour dessiner L k..
- Déterminer la complexité de votre méthode de dessin.
A RENDRE |
|
III- Troisième famille: E k
On défini E0 comme étant vide, En est formé de 5 segments. Les 5 segments ont une extrémité commune, deux segments "consécutifs" forment un angle de 72°, la deuxième extrémité de chacun des segments est le centre d'une copie de En-1
Remarque : la longueur des segments doit dépendre de n, à vous de voir comment....
Voici E1 et E3
![[5 Lines Radiating from a Center]](MiniProjet/Images/star1.gif)
![[Star with Stars with Stars on the Ends of the Lines]](MiniProjet/Images/star3.gif)
Et voici une version modifiée de E5, où l'on a utilisé 7 segments au lieu de 5
![[Lace-Like Pattern]](MiniProjet/Images/star5.gif)
Questions
- Ecrire une méthode récursive pour dessiner E k..
- Déterminer la complexité de votre méthode de dessin.
A RENDRE |
|